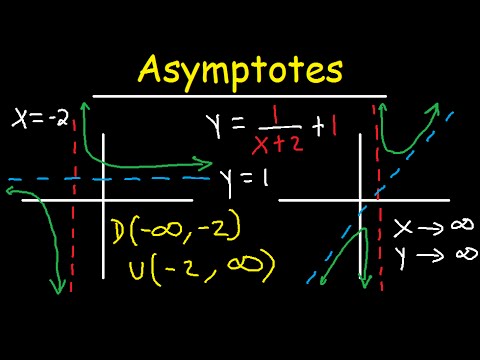
Q. Do reciprocal functions have Asymptotes?
Asymptote. Given a function and the corresponding reciprocal function, the graph of the reciprocal function will have vertical asymptotes where the function has zeros (the x-intercept(s) of the graph of the function). f(x) = ( x – 3 )2 – 4. The graph of a function will never have more than one horizontal asymptote.
Q. Do trigonometric functions have Asymptotes?
1 Answer. tanx , cotx , secx , and cscx have vertical asymptotes.
Table of Contents
- Q. Do reciprocal functions have Asymptotes?
- Q. Do trigonometric functions have Asymptotes?
- Q. How do you find the asymptote of a reciprocal function?
- Q. Can Asymptotes be zero?
- Q. How do you know if there are no vertical asymptotes?
- Q. Can you have a point on an asymptote?
- Q. Are functions defined at Asymptotes?
- Q. How do you find a point of inflection?
- Q. Can you have 3 vertical asymptotes?
- Q. Why do vertical asymptotes occur?
- Q. Which has a vertical asymptote exponential or logarithmic?
- Q. What is the limit of a vertical asymptote?
- Q. When can a limit not exist?
- Q. Do limits exist at jump discontinuities?
- Q. What is the difference between a limit and an asymptote?
- Q. How do you find the limits of Asymptotes?
- Q. What is an infinite limit?
- Q. Do limits exist at horizontal asymptotes?
- Q. What is the maximum number of horizontal asymptotes?
- Q. Are Asymptotes limits?
- Q. How would you know a limit resulted in a horizontal asymptote?
- Q. What is the horizontal asymptote of this graph?
- Q. What does it mean to have a horizontal asymptote?
- Q. How do you graph vertical and horizontal asymptotes?
- Q. Which graph represents a function How do you know?
- Q. How do you find the horizontal asymptote of a graph?
- Q. What are the rules for vertical asymptotes?
- Q. What is the equation of the horizontal asymptote?
Q. How do you find the asymptote of a reciprocal function?
To do this we need to look at the degrees of the polynomials. Let m=degree of p(x)n=degree of q(x) 1. If m”>n>m then the horizontal asymptote is y=0 2. If n=m then the horizontal asymptote is y=ab where a is the lead coefficient of p(x) and b is the lead coefficient of q(x) 3.
Q. Can Asymptotes be zero?
You can have a vertical asymptote where both the numerator and denominator are zero. You don’t always have an asymptote just because you have a 0/0 expression. This limit is ±∞ (depending on the side and so x=3 is an vertical asymptote.
Q. How do you know if there are no vertical asymptotes?
Vertical asymptote of a rational function occurs when denominator is becoming zeroes. If a function like any polynomial y=x2+x+1 has no vertical asymptote at all because the denominator can never be zeroes. although x≠a. However, if x is defined on a then there is no removable discontinuity.
Q. Can you have a point on an asymptote?
Note that by common understanding, a point where a function is undefined, like a vertical asymptote, is not included in its domain. Therefore, a function can have a vertical asymptote and still be a continuous function.
Q. Are functions defined at Asymptotes?
A vertical asymptote occurs where the function is undefined (e.g., the function is y=A/B, set B=0). A horizontal asymptote (or oblique) is determined by the limit of the function as the independent variable approaches infinity and negative infinity.
Q. How do you find a point of inflection?
Inflection points are points where the function changes concavity, i.e. from being “concave up” to being “concave down” or vice versa. They can be found by considering where the second derivative changes signs.
Q. Can you have 3 vertical asymptotes?
A graph can have an infinite number of vertical asymptotes, but it can only have at most two horizontal asymptotes. Horizontal asymptotes describe the left and right-hand behavior of the graph. A graph will (almost) never touch a vertical asymptote; however, a graph may cross a horizontal asymptote.
Q. Why do vertical asymptotes occur?
Vertical asymptotes occur when a factor of the denominator of a rational expression does not cancel with a factor from the numerator. When you have a factor that does not cancel, instead of making a hole at that x value, there exists a vertical asymptote.
Q. Which has a vertical asymptote exponential or logarithmic?
A logarithmic function will have the domain as (0, infinity). The range of a logarithmic function is (−infinity, infinity). The logarithmic function graph passes through the point (1, 0), which is the inverse of (0, 1) for an exponential function. The graph of a logarithmic function has a vertical asymptote at x = 0.
Q. What is the limit of a vertical asymptote?
The vertical asymptote is a place where the function is undefined and the limit of the function does not exist. This is because as 1 approaches the asymptote, even small shifts in the x -value lead to arbitrarily large fluctuations in the value of the function.
Q. When can a limit not exist?
Limits typically fail to exist for one of four reasons: The one-sided limits are not equal. The function doesn’t approach a finite value (see Basic Definition of Limit). The function doesn’t approach a particular value (oscillation).
Q. Do limits exist at jump discontinuities?
The limit of a function doesn’t exist at a jump discontinuity, since the left- and right-hand limits are unequal.
Q. What is the difference between a limit and an asymptote?
A limit is the value that the output of a function approaches as the input of the function approaches a given value. An oblique asymptote is a diagonal line marking a specific range of values toward which the graph of a function may approach, but generally never reach.
Q. How do you find the limits of Asymptotes?
A function f(x) will have the horizontal asymptote y=L if either limx→∞f(x)=L or limx→−∞f(x)=L. Therefore, to find horizontal asymptotes, we simply evaluate the limit of the function as it approaches infinity, and again as it approaches negative infinity.
Q. What is an infinite limit?
The statement limx→af(x)=∞ tells us that whenever x is close to (but not equal to) a, f(x) is a large positive number. A limit with a value of ∞ means that as x gets closer and closer to a, f(x) gets bigger and bigger; it increases without bound.
Q. Do limits exist at horizontal asymptotes?
there’s no horizontal asymptote and the limit of the function as x approaches infinity (or negative infinity) does not exist.
Q. What is the maximum number of horizontal asymptotes?
two
Q. Are Asymptotes limits?
The limit of a function, f(x), is a value that the function approaches as x approaches some value. A one-sided limit is a limit in which x is approaching a number only from the right or only from the left. An asymptote is a line that a graph approaches but doesn’t touch.
Q. How would you know a limit resulted in a horizontal asymptote?
For a rational function f(x)=p(x)q(x), the Limit at infinity is determined by the relationship between the degree of p and the degree of q. If the degree of p is less than the degree of q, the line y=0 is a horizontal asymptote for f.
Q. What is the horizontal asymptote of this graph?
Horizontal asymptotes are horizontal lines the graph approaches. To find horizontal asymptotes: If the degree (the largest exponent) of the denominator is bigger than the degree of the numerator, the horizontal asymptote is the x-axis (y = 0).
Q. What does it mean to have a horizontal asymptote?
A horizontal asymptote is a horizontal line that indicates where a function flattens out as the independent variable gets very large or very small. A function may touch or pass through a horizontal asymptote. Intercept. The intercepts of a curve are the locations where the curve intersects the x and y axes.
Q. How do you graph vertical and horizontal asymptotes?
Process for Graphing a Rational Function
- Find the intercepts, if there are any.
- Find the vertical asymptotes by setting the denominator equal to zero and solving.
- Find the horizontal asymptote, if it exists, using the fact above.
- The vertical asymptotes will divide the number line into regions.
- Sketch the graph.
Q. Which graph represents a function How do you know?
How To: Given a graph, use the vertical line test to determine if the graph represents a function.
- Inspect the graph to see if any vertical line drawn would intersect the curve more than once.
- If there is any such line, the graph does not represent a function.
Q. How do you find the horizontal asymptote of a graph?
The horizontal asymptote of a rational function can be determined by looking at the degrees of the numerator and denominator.
- Degree of numerator is less than degree of denominator: horizontal asymptote at y = 0.
- Degree of numerator is greater than degree of denominator by one: no horizontal asymptote; slant asymptote.
Q. What are the rules for vertical asymptotes?
To determine the vertical asymptotes of a rational function, all you need to do is to set the denominator equal to zero and solve. Vertical asymptotes occur where the denominator is zero. Remember, division by zero is a no-no. Because you can’t have division by zero, the resultant graph thus avoids those areas.
Q. What is the equation of the horizontal asymptote?
Another way of finding a horizontal asymptote of a rational function: Divide N(x) by D(x). If the quotient is constant, then y = this constant is the equation of a horizontal asymptote.