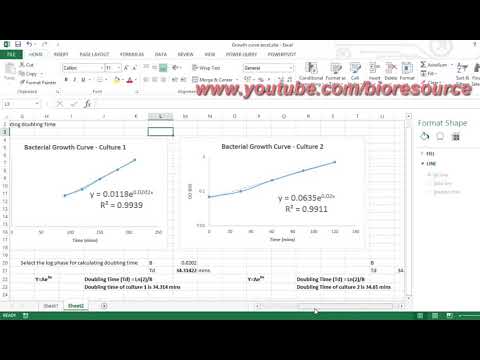
The doubling time is given by log(2)/m, where m is the estimate of the slope of the cumulative curve in a semi-log graph. If you want to visualize the doubling time on the graph, you can add an arrow to the end of each curve.
Q. What is the doubling time equation for exponential growth?
We can find the doubling time for a population undergoing exponential growth by using the Rule of 70. To do this, we divide 70 by the growth rate (r). Note: growth rate (r) must be entered as a percentage and not a decimal fraction. For example 5% must be entered as 5 instead of 0.05.
Table of Contents
- Q. What is the doubling time equation for exponential growth?
- Q. What is the equation for exponential population growth?
- Q. How do you find doubling time in math?
- Q. Why is the number 70 used for doubling time?
- Q. Why do you use 70 in doubling time?
- Q. How many years will it take for a population to double if its growth rate is 1 %?
- Q. Why is doubling time useful?
- Q. What Is percent Doubling?
- Q. Is 50% or 100% double?
- Q. Is 200% a double?
- Q. How do you calculate 100 increase?
- Q. Is doubling a 100 percent increase?
- Q. What is the percent of increase from 5 to 8?
- Q. What is the percent of decrease from 500000 to 50000?
Q. What is the equation for exponential population growth?
In this equation, d N / d T dN/dT dN/dTd, N, slash, d, T is the growth rate of the population in a given instant, N is population size, T is time, and r is the per capita rate of increase –that is, how quickly the population grows per individual already in the population.
Q. How do you find doubling time in math?
Doubling time formula doubling time = log(2) / log(1 + increase) , where: increase is the constant growth rate expressed as a percentage value, doubling time is the time needed for the quantity to double in value for a specified constant growth rate.
Q. Why is the number 70 used for doubling time?
The Rule of 70 is commonly used in accounting and finance as a way of estimating the number of years (t) it will take for the principal investment (P) to double in value given a particular interest rate (r) and an annual compounding period. The Rule of 70 says that the doubling time is close to .
Q. Why do you use 70 in doubling time?
The rule of 70 is a calculation to determine how many years it’ll take for your money to double given a specified rate of return. The rule is commonly used to compare investments with different annual compound interest rates to quickly determine how long it would take for an investment to grow.
Q. How many years will it take for a population to double if its growth rate is 1 %?
about 63 years
Q. Why is doubling time useful?
Doubling time is the time it takes for something, growing at a steady rate, to double in size. The reason it is so important is because doubling (or halving) is a much easier concept for us to comprehend whereas the exponent itself may not be.
Q. What Is percent Doubling?
An increase of 100% in a quantity means that the final amount is 200% of the initial amount (100% of initial + 100% of increase = 200% of initial). In other words, the quantity has doubled. An increase of 800% means the final amount is 9 times the original (100% + 800% = 900% = 9 times as large).
Q. Is 50% or 100% double?
A 50% increase is different to a 100% increase, which is double the original value.
Q. Is 200% a double?
A percentage is a dimensionless number (pure number). 100% is double. 200% is triple. 300% is quadruple.
Q. How do you calculate 100 increase?
Percentage Change | Increase and Decrease
- First: work out the difference (increase) between the two numbers you are comparing.
- Increase = New Number – Original Number.
- Then: divide the increase by the original number and multiply the answer by 100.
- % increase = Increase ÷ Original Number × 100.
Q. Is doubling a 100 percent increase?
Yes, doubling a number is the same as multiplying in by two or by increasing it by 100%. Here is another way of looking at this: 50 increased by 100% of 50 is 100. You can express this mathematically: 50+ 50(100/100) = 100.
Q. What is the percent of increase from 5 to 8?
60
Q. What is the percent of decrease from 500000 to 50000?
90.5%