Q. How do you prove Cos double angle?
The double-angle formulas are simple to prove, once the Addition Formulas for Sine and Cosine are in place. By the Pythagorean Identity, cos2x=1−sin2x x = 1 − sin 2 and sin2x=1−cos2x x = 1 − cos 2 .
Q. What is the double angle formula for cos?
The cosine double angle formula tells us that cos(2θ) is always equal to cos²θ-sin²θ. For example, cos(60) is equal to cos²(30)-sin²(30).
Table of Contents
- Q. How do you prove Cos double angle?
- Q. What is the double angle formula for cos?
- Q. What are the formulas for cos2A?
- Q. Can you rewrite cos 2x?
- Q. What is the formula of sin 2A?
- Q. What are the formulas of Cos 2A?
- Q. Which is the proof of the COS double angle identity?
- Q. How to prove the double angle formula in trigonometry?
- Q. Which is the correct formula for cos 2A?
- Q. How to get the COs of double angle?
Q. What are the formulas for cos2A?
The formula cos 2A = cos2 A − sin so that by rearrangement sin2 A = 1 − cos2 A.
Q. Can you rewrite cos 2x?
The double-angle formula for cosine comes from the sum formula, just like the double-angle formula for sine. If you can’t remember the double-angle formula but you can remember the sum formula, just rewrite cos(2x) as cos(x + x). You can replace cos2 x with (1 – sin2 x) and simplify to get cos 2x = 1 – 2 sin2 x.
Q. What is the formula of sin 2A?
The general formula of sin 2A is, sin 2A = 2 sin A cos A. Using sin2A + cos2A = 1, we get cos A =√(1 – sin2A). Substituting this in the above formula, sin 2A = 2 sin A √(1 – sin2A).
Q. What are the formulas of Cos 2A?
FAQs on Double Angle Formulas sin 2A = 2 sin A cos A. cos 2A = cos2A – sin2A. tan 2A = (2 tan A) / (1 – tan2A)
Q. Which is the proof of the COS double angle identity?
Proof of Cos double angle identity. The cos double angle identity is a mathematical formula in trigonometry and used to expand cos functions which contain double angle. For example, if theta ( θ) is angle of a right triangle, then the cos of double angle is written as θ cos. ( 2 θ). It is expanded mathematically as follows.
Q. How to prove the double angle formula in trigonometry?
Trigonometry from the very beginning. The double-angle formulas are proved from the sum formulas by putting β = . We have 2 sin cos . cos 2 − sin 2. . . . . . .
Q. Which is the correct formula for cos 2A?
It would be nice to have a formula for cos 2A in terms of just a sine or just a cosine. Fortunately, we can use sin² x + cos² x = 1 to eliminate either the sine or the cosine from that formula: cos 2A = cos² A − sin² A = cos² A − (1 − cos² A) = 2 cos² A − 1.
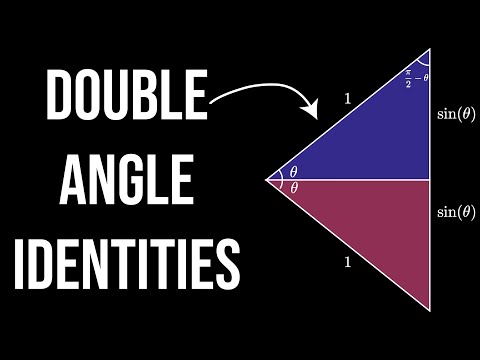
Q. How to get the COs of double angle?
The cos of double angle identity can be derived in trigonometry by constructing a right triangle with double angle. Follow the below steps to get the requisite triangle. The angle of Δ F D E is bisected by the straight line drawn from point D to side E F ― and it intersects the side E F ― at point G.