When you reflect a point across the line y = x, the x-coordinate and y-coordinate change places. If you reflect over the line y = -x, the x-coordinate and y-coordinate change places and are negated (the signs are changed). the line y = x is the point (y, x). the line y = -x is the point (-y, -x).
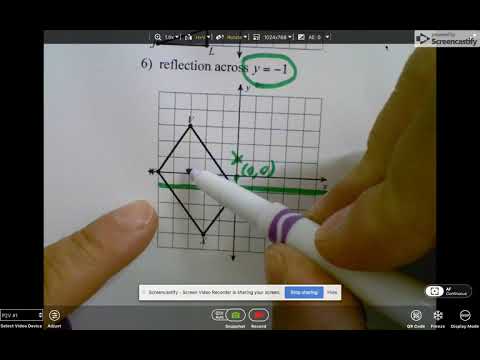
Q. What does it mean to reflect over Y 1?
Explanation: the line y=1 is a horizontal line passing through all. points with a y-coordinate of 1. the point (3,10) reflected in this line. the x-coordinate remains in the same position.
Table of Contents
- Q. What does it mean to reflect over Y 1?
- Q. What are the rules for reflection?
- Q. What is the formula of reflection?
- Q. How do you find the Y intercept of a reflection?
- Q. What are the rules for transformations?
- Q. What are the three basic types of function transformations?
- Q. How do you calculate transformations?
- Q. How do you describe reflection transformation?
- Q. How do you describe graph transformations?
- Q. What order do you apply transformations?
- Q. What are the four transformations in maths?
- Q. How can you use transformations in real life?
- Q. What does transformation mean in math?
- Q. What is the scientific meaning of transformation?
- Q. What does it mean to transform a shape?
- Q. What is the purpose of transformation in biology?
- Q. What is transformation used for in biology?
- Q. What was Avery’s conclusion?
Q. What are the rules for reflection?
Reflection on a Coordinate Plane
- Reflection Over X Axis. When reflecting over (across) the x-axis, we keep x the same, but make y negative.
- Reflection Over Y Axis. When reflecting over (across) the y-axis, we keep y the same, but make x-negative.
- Reflection Across Y=X.
- Reflection Across Y=-X.
Q. What is the formula of reflection?
A reflection of a point over the x -axis is shown. The rule for a reflection over the x -axis is (x,y)→(x,−y) .
Q. How do you find the Y intercept of a reflection?
To find the reflection of the y intercept, duplicate the y value of the point and find the x distance to the AOS then travel the same distance on the other side of the AOS. In this case, the y value of the reflection of the y intercept, (0, -1) is –1, so the reflected point will also have a y value of –1.
Q. What are the rules for transformations?
The function translation / transformation rules:
- f (x) + b shifts the function b units upward.
- f (x) – b shifts the function b units downward.
- f (x + b) shifts the function b units to the left.
- f (x – b) shifts the function b units to the right.
- –f (x) reflects the function in the x-axis (that is, upside-down).
Q. What are the three basic types of function transformations?
A transformation takes a basic function and changes it slightly with predetermined methods. This change will cause the graph of the function to move, shift, or stretch, depending on the type of transformation. The four main types of transformations are translations, reflections, rotations, and scaling.
Q. How do you calculate transformations?
Example: the function g(x) = 1/x
- Move 2 spaces up:h(x) = 1/x + 2.
- Move 3 spaces down:h(x) = 1/x − 3.
- Move 4 spaces right:h(x) = 1/(x−4) graph.
- Move 5 spaces left:h(x) = 1/(x+5)
- Stretch it by 2 in the y-direction:h(x) = 2/x.
- Compress it by 3 in the x-direction:h(x) = 1/(3x)
- Flip it upside down:h(x) = −1/x.
Q. How do you describe reflection transformation?
A reflection is a type of transformation. It ‘maps’ one shape onto another. When a shape is reflected a mirror image is created. If the shape and size remain unchanged, the two images are congruent.
Q. How do you describe graph transformations?
| Transformations of Function Graphs | |
|---|---|
| -f (x) | reflect f (x) over the x-axis |
| f (x – k) | shift f (x) right k units |
| k•f (x) | multiply y-values by k (k > 1 stretch, 0 < k < 1 shrink vertical) |
| f (kx) | divide x-values by k (k > 1 shrink, 0 < k < 1 stretch horizontal) |
Q. What order do you apply transformations?
Apply the transformations in this order:
- Start with parentheses (look for possible horizontal shift) (This could be a vertical shift if the power of x is not 1.)
- Deal with multiplication (stretch or compression)
- Deal with negation (reflection)
- Deal with addition/subtraction (vertical shift)
Q. What are the four transformations in maths?
The following figures show the four types of transformations: Translation, Reflection, Rotation, and Dilation.
Q. How can you use transformations in real life?
One real world example of transformations is with planes. A plane at Takeoff is the same size and shape of the same plane while landing or on the runway. It is just a Translation since the plane is just in a different angle.
Q. What does transformation mean in math?
Transformations. Transformation means to change. Hence, a geometric transformation would mean to make some changes in any given geometric shape.
Q. What is the scientific meaning of transformation?
noun, plural: transformations. (1) The act, state or process of changing, such as in form or structure; the conversion from one form to another. (2) (biology) Any change in an organism that alters its general character and mode of life; post-natal biological transformation or metamorphosis.
Q. What does it mean to transform a shape?
A transformation is a process that manipulates a polygon or other two-dimensional object on a plane or coordinate system. Mathematical transformations describe how two-dimensional figures move around a plane or coordinate system. A preimage or inverse image is the two-dimensional shape before any transformation.
Q. What is the purpose of transformation in biology?
Transformation of cells is a widely used and versatile tool in genetic engineering and is of critical importance in the development of molecular biology. The purpose of this technique is to introduce a foreign plasmid into bacteria, the bacteria then amplifies the plasmid, making large quantities of it.
Q. What is transformation used for in biology?
Transformation enables the expression of multiple copies of DNA resulting in large amounts of protein or enzyme that are not normally expressed by bacteria. Genetic material of transformed bacteria may be used to transfect eukaryotic cells for DNA or protein expression studies.
Q. What was Avery’s conclusion?
Oswald Avery, Colin MacLeod, and Maclyn McCarty showed that DNA (not proteins) can transform the properties of cells, clarifying the chemical nature of genes. Avery, MacLeod and McCarty identified DNA as the “transforming principle” while studying Streptococcus pneumoniae, bacteria that can cause pneumonia.