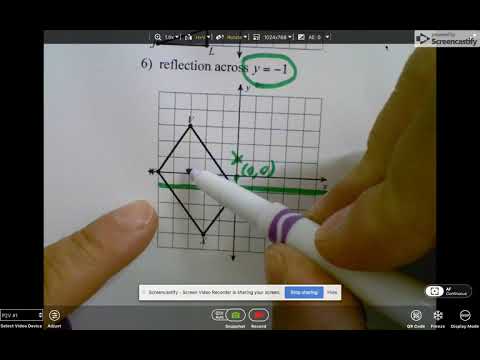
The line y=-1 is a horizontal line and thus is a line that is parallel to the x-axis. If we reflect about a line that is parallel to the x-axis, then the x-coordinate of the point (that is reflected) will remain the same, thus the image of (2,-4) has x-coordinate 2 and thus the point is of the form (2,b).

The law of reflection states that the angle of reflection equals the angle of incidence—θr = θi. The angles are measured relative to the perpendicular to the surface at the point where the ray strikes the surface.

Explanation: the line y=1 is a horizontal line passing through all. points with a y-coordinate of 1. the point (3,10) reflected in this line. the x-coordinate remains in the same position.

When you reflect a point across the y-axis, the y-coordinate remains the same, but the x-coordinate is transformed into its opposite (its sign is changed). Remember that each point of a reflected image is the same distance from the line of reflection as the corresponding point of the original figure.

The positive regions of a function are those intervals where the function is above the x-axis. It is where the y-values are positive (not zero). The negative regions of a function are those intervals where the function is below the x-axis.

Always use a parenthesis, not a bracket, with infinity or negative infinity. You also use parentheses for 2 because at 2, the graph is neither increasing or decreasing – it is completely flat. To find the intervals where the graph is negative or positive, look at the x-intercepts (also called zeros).

Explanation: To find the increasing intervals of a given function, one must determine the intervals where the function has a positive first derivative. To find these intervals, first find the critical values, or the points at which the first derivative of the function is equal to zero.

In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers x satisfying 0 ≤ x ≤ 1 is an interval which contains 0, 1, and all numbers in between.

The derivative of a function may be used to determine whether the function is increasing or decreasing on any intervals in its domain. If f′(x) > 0 at each point in an interval I, then the function is said to be increasing on I. f′(x) < 0 at each point in an interval I, then the function is said to be decreasing on I.

• A graph is called an interval graph if each of its vertices can be associated with an interval on the real line in such a way that two vertices are adjacent if and only if the associated intervals have a nonempty intersection. These intervals are said to form an interval representation of the graph.

In “Interval Notation” we just write the beginning and ending numbers of the interval, and use:

1. [ ] a square bracket when we want to include the end value, or.
2. ( ) a round bracket when we don’t.