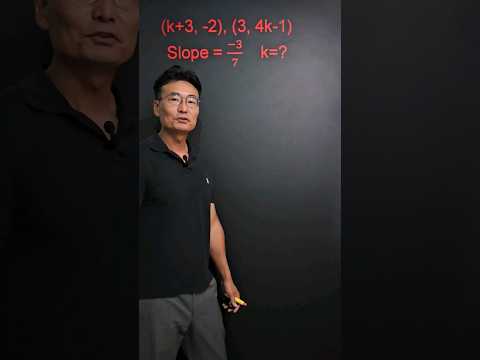h – represents the change in x or (x2 – x1) or ∆x f (x+h) – f (x) – represents (y2 – y1)

Derivative by first principle refers to using algebra to find a general expression for the slope of a curve It is also known as the delta method The derivative is a measure of the instantaneous rate of change, which is equal to f ′ ( x ) = lim ⁡ h → 0 f ( x + h ) − f ( x ) h

In such formulae h is usually a “very small number”, similar to epsilon in Calculus For example, the derivative of f at a is defined as: Note how h is defined as approaching 0

One type of notation for derivatives is sometimes called prime notation The function f ´( x ), which would be read “ f -prime of x ”, means the derivative of f ( x ) with respect to x If we say y = f ( x ), then y ´ (read “ y -prime”) = f ´( x )

7 Answers If f(x) is a (real) function (of a real variable), then its derivative f′(a) at a point a measures the sensitivity of f to small changes in x around a The derivative gives us a way to quantify this observation

The Quotient Rule d (u/v) = v(du/dx) – u(dv/dx)

We use the derivative to determine the maximum and minimum values of particular functions (eg cost, strength, amount of material used in a building, profit, loss, etc) Derivatives are met in many engineering and science problems, especially when modelling the behaviour of moving objects

Without the use of calculus roads, bridges, tunnels would not be safe as they are today 4) Biologist also makes use of calculus in many applications They use calculus concepts to determine the growth rate of bacteria, modeling population growth and so on In medical field also calculus is useful

Limits are also used as real-life approximations to calculating derivatives So, to make calculations, engineers will approximate a function using small differences in the a function and then try and calculate the derivative of the function by having smaller and smaller spacing in the function sample intervals

Definition: A derivative is a contract between two parties which derives its value/price from an underlying asset The most common types of derivatives are futures, options, forwards and swaps Description: It is a financial instrument which derives its value/price from the underlying assets

If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) <0 on an interval, then f is decreasing on that interval If f'(x)=0, then the x value is a point of inflection for f

Yes, as long as x is the variable you are differentiating with respect to For example, if your function is y = 3x 2 + 5x, then both y′ and dy/dx refer to the derivative of this function with respect to x, which is 6x + 5

yes they mean the exact same thing; y’ in newtonian notation and dy/dx is leibniz notation Newton and Leibniz independently invented calculus around the same time so they used different notation to represent the same thing (rate of change in this case)

Derivatives as dy/dx

1. Add Δx When x increases by Δx, then y increases by Δy : y + Δy = f(x + Δx)
2. Subtract the Two Formulas From: y + Δy = f(x + Δx) Subtract: y = f(x) To Get: y + Δy − y = f(x + Δx) − f(x) Simplify: Δy = f(x + Δx) − f(x)
3. Rate of Change

Δy represents the y increment along the curve It depends on the shape of the curve dydx is the slope of the tangent, ie the derivative

the rate of change of y