Q. What is the energy of a particle in an one-dimensional box?
The energy of a particle is quantized. This means it can only take on discreet energy values. The lowest possible energy for a particle is NOT zero (even at 0 K). This means the particle always has some kinetic energy.
Q. What is the value of minimum energy of particle in one-dimensional box?
zero
The lowest possible energy of a particle is NOT zero. This is called the zero-point energy and means the particle can never be at rest because it always has some kinetic energy.
Table of Contents
- Q. What is the energy of a particle in an one-dimensional box?
- Q. What is the value of minimum energy of particle in one-dimensional box?
- Q. How can you explain that energy in one-dimensional box is quantized?
- Q. When N 3 What is the energy of a particle in one dimensional box?
- Q. Which of the following is the correct expression for the group velocity?
- Q. How do you calculate Eigenstate energy?
- Q. What is the minimum energy of a particle?
- Q. Which of the following is the correct expression for the Schrödinger wave function *?
- Q. Which of the following is known as the Schrödinger equation?
- Q. How do you find the energy of a wave function?
- Q. Which of the following wave function is the solution of Schrödinger equation?
- Q. How is the energy of a particle quantized in a box?
- Q. What happens to a particle inside a box?
- Q. What is the Schrodinger equation for a particle in a box?
- Q. How to calculate the energy of a particle?
Q. How can you explain that energy in one-dimensional box is quantized?
The energy of the particle is quantized as a consequence of a standing wave condition inside the box. The potential energy function that confines the particle in a one-dimensional box. A particle bound to a one-dimensional box can only have certain discrete (quantized) values of energy.
Q. When N 3 What is the energy of a particle in one dimensional box?
where h is the Planck constant, m is the mass of a particle, and L is the dimension (length) of the box. So for n=1, n=2 and n=3 the energy values will be h2/8mL2, h2/2mL2 and 9h2/8mL2 respectively.
Q. Which of the following is the correct expression for the group velocity?
Which of the following is the correct expression for the group velocity? Explanation: The velocity with which the wave packet moves is called the group velocity. It is equal to dω/dk, which can be further simplified to dE/ħdk, as E =ħω. 5.
Q. How do you calculate Eigenstate energy?
Review of Time Dependence Remember: You can always write an energy eigenstate as Ψ(x,t) = ψ(x)e–iEt/1. Probability density = |Ψ(x,t)|2 = Ψ(x,t)Ψ*(x,t) = ψ(x)e–iEt/1ψ*(x)e+iEt/1 = ψ(x)ψ*(x) = |ψ(x)|2 ⇒ wave function has time dependence in phase.
Q. What is the minimum energy of a particle?
In particle physics, the threshold energy for production of a particle is the minimum kinetic energy a pair of traveling particles must have when they collide. The threshold energy is always greater than or equal to the rest energy of the desired particle.
Q. Which of the following is the correct expression for the Schrödinger wave function *?
Which of the following is the correct expression for the Schrödinger wave function? Explanation: The correct expression for the Schrödinger wave equation is i/hbar /frac{d/Psi}{dt}= -i/frac{/hbar^z}{2m} /frac{/partial^2/Psi}{/partial x^2}+ U/Psi . Schrodinger equation is a basic principle in itself.
Q. Which of the following is known as the Schrödinger equation?
The Schrödinger equation is the fundamental equation of physics for describing quantum mechanical behavior. It is also often called the Schrödinger wave equation, and is a partial differential equation that describes how the wavefunction of a physical system evolves over time.
Q. How do you find the energy of a wave function?
The wavefunction of a light wave is given by E(x,t), and its energy density is given by |E|2, where E is the electric field strength. The energy of an individual photon depends only on the frequency of light, ϵphoton=hf, so |E|2 is proportional to the number of photons.
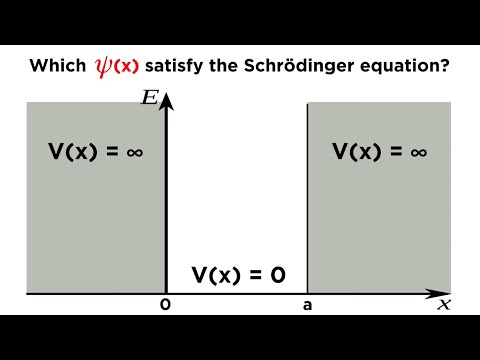
Q. Which of the following wave function is the solution of Schrödinger equation?
The wave function Ψ(x, t) = Aei(kx−ωt) represents a valid solution to the Schrödinger equation. The wave function is referred to as the free wave function as it represents a particle experiencing zero net force (constant V ).
Q. How is the energy of a particle quantized in a box?
The energy of the particle is quantized as a consequence of a standing wave condition inside the box. Consider a particle of mass that is allowed to move only along the x -direction and its motion is confined to the region between hard and rigid walls located at and at ( (Figure) ).
Q. What happens to a particle inside a box?
The particle has only kinetic energy and no potential energy inside the box. Therefore, inside the box . (The particle wave function is dependent on only one coordinate, therefore, only x coordinate and likewise x component only for momentum p ).
Q. What is the Schrodinger equation for a particle in a box?
Particle in a one dimensional box. Schrodinger Equation for a particle-in-a-box: Confine a particle to a finite region in which it has no potential energy. Its energy is only due to motion—-kinetic energy. It experiences no potentials due to any external force, i.e., its potential energy is zero inside the region.
Q. How to calculate the energy of a particle?
The energy operator ^E E ^ associated with this particle is the one with eigenvalues Ei = p2 2m E i = p 2 2 m. This operator is given by ^E = ^p2 2m. (2) (2) E ^ = p ^ 2 2 m.
https://www.youtube.com/watch?v=uPvWlwOhCTo