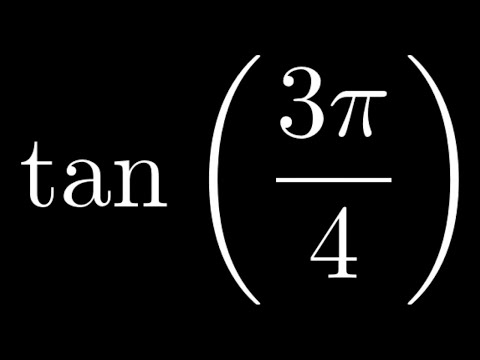1 Answer

1. tan(3π4)=sin(3π4)cos(3π4) Knowing the unit circle, we can see that.
2. sin(3π4)=√22. and.
3. cos(3π4)=−√22. so. tan(3π4)=(√22)⋅(−2√2)((−√22)⋅(−2√2))

quadrant two
tan(3π4) equals what? It equals -1 on the unit circle. This is because tan uses both sine and cosine ( sincos ) and in quadrant two, which 3π4 sits in only cosine is negative making tangent a negative.

135 degrees
The degree form when we convert $/dfrac{{3/pi }}{4}$ radians to degrees is equal to 135 degrees.

Tan 3pi/4 radians in degrees is written as tan ((3π/4) × 180°/π), i.e., tan (135°)….We can use trigonometric identities to represent tan 3pi/4 as,

1. cot(pi/2 – 3pi/4) = cot(-pi/4)
2. -cot(pi/2 + 3pi/4) = -cot 5pi/4.
3. -tan (pi – 3pi/4) = -tan pi/4.

By the trig unit circle. tan(3π4)=−tan(π4)=−1 .

Therefore by substitution 3×π4 is equal to 3×1804 which equals 135 degrees. I hope this helps!

Tan 135 degrees can also be expressed using the equivalent of the given angle (135 degrees) in radians (2.35619 . . .) ⇒ 135 degrees = 135° × (π/180°) rad = 3π/4 or 2.3561 . . . Since the tangent function is a periodic function, we can represent tan 135° as, tan 135 degrees = tan(135° + n × 180°), n ∈ Z.

tan(3π4)=−tan(π4)=−1 .

-1
The value of cot 3pi/4 is -1. Cot 3pi/4 radians in degrees is written as cot ((3π/4) × 180°/π), i.e., cot (135°).

To find the exact value of sin(135), you need the following formula: sin (a+b) = sin a • cos b – cos a + sin b So in this case, it would be sin (135) = sin (90 + 45) = sin 90 • cos 45 + cos 90 • sin 45 = (1 ·(√2)/2) + (0 · (√2)/2) = (√2)/2). cos (135)= – (√2)/2 and sin (135) = (√2)/2. Log in to add a comment.

The exact value of tan (60) tan ( 60) is √3 3. Apply the reference angle by finding the angle with equivalent trig values in the first quadrant. Make the expression negative because tangent is negative in the second quadrant. The exact value of tan (30) tan ( 30) is √33 3 3. Tap for more steps… Multiply 3 3 by 1 1.

How to find the reference angle for degrees. All you have to do is follow these steps: Choose your initial angle – for example, 610°. If your angle is larger than 360° (a full angle), subtract 360°. Keep doing it until you get an angle smaller than a full angle. This is the same as finding the modulo.

With just the opposite and adjacent sides, you can calculate the angle at the base of the ladder using the arctangent function. If the wall (opposite) side is 10 feet, and the ground (adjacent) side is 5 feet, the formula for the tangent angle is the opposite side divided by the adjacent side. This is 10 divided by 5, or 0.5.