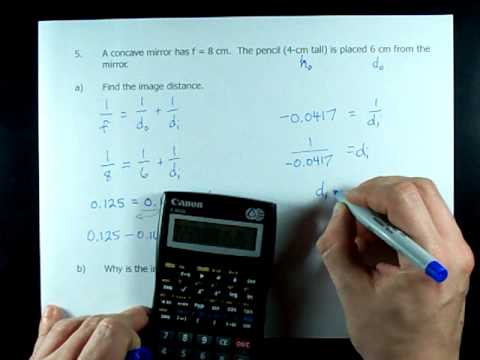Answer: A 7.00 cm tall object placed 30.0 cm from a concave mirror having a focal length of 10.0 cm has an image distance of 15.0 cm and an image height of 3.5 cm.
Q. What is height of image for a concave mirror?
hi = -1.99 cm From the calculations in this problem it can be concluded that if a 4.00-cm tall object is placed 45.7 cm from a concave mirror having a focal length of 15.2 cm, then the image will be inverted, 1.99-cm tall and located 22.8 cm from the mirror.
Q. How do you find the height of an object?
3 Answers. You can calculate the height of an object using the distance and angle. distance * cos(angle), where distance is the horizontal distance to the object, and angle is the angle above horizontal of the top of the object (from the viewer). The result will be the height above the viewer.
Q. How do you find the height of an object on a calculator?
The height of an object is calculated by measuring the distance from the object and the angle of elevation of the top of the object. The tangent of the angle is the object height divided by the distance from the object. Thus, the height is found.
Q. How do you find the height of a tall object?
To determine the height of an object, the distance from the observer to the object is first measured using a meter stick or tape measure. Next, angle θ is measured with a clinometer. The line of sight is determined by looking through a tube or site on the clinometer.
Q. How do you find the height of an angle of depression?
The angle of depression may be found by using this formula: tan y = opposite/adjacent. The opposite side in this case is usually the height of the observer or height in terms of location, for example, the height of a plane in the air. The adjacent is usually the horizontal distance between the object and the observer.
Q. What is an angle of depression in geometry?
The term angle of depression denotes the angle from the horizontal downward to an object. An observer’s line of sight would be below the horizontal. Note that the angle of elevation and the angle of depression are congruent .
Q. What is the angle of depression in a triangle?
The “downwards” angle from the horizontal to a line of sight from the observer to some point of interest. If the angle goes “upwards” it is called an Angle of Elevation.
Q. What is the relationship between an angle of elevation and an angle of depression in a right triangle?
Angles of elevation and depression are angles that are formed with the horizontal. If the line of sight is upward from the horizontal, the angle is an angle of elevation; if the line of sight is downward from the horizontal, the angle is an angle of depression.
Q. Which are the angles of depression from the observing positions A and C?
Solution. Hence the required angles are 30 ° 45 ° .
Q. What are the angles of depression from the observing?
Answer. The angles of depressions are 30 degree n 45 degrees resp.
Q. What are angles of depression from observing positions o1 and o2?
Answer. Hence the required angles are 30o, 45o.
Q. What are the angles of depression from the observing positions o1 and o2 of the object at a?
Some Applications of Trigonometry. In the following figure, what are the angles of depression from the observing positions O1 and O2 of the object at A? From O1 and O2 draw the dotted lines parallel to ABC, then the angle of depression from the positions O1 and O2 of the object at A are 30° and 45°, respectively.
Q. What are the angle of depression from the observing position D and E of the object A?
Now , EX ∥ AC and AE is a transversal , then ∠ AEX = ∠ EAC Alternate interior angles In ∆ ACE , ∠ EAC + ∠ ACE + ∠ AEC = 180 ° Angle sum property ⇒ ∠ EAC + 90 ° + 60 ° = 180 ° ⇒ ∠ EAC = 30 ° So , ∠ AEX = 30 ° Hence , the angle of depressions of the object at A from point D and E are 45 ° and 30 ° .
Q. When the length of the shadow of a pole of height 10 m?
Answer. The source of light must at an angle of 45 degrees that is why the length of the shadow is equal to the length of the ploe.
Q. When the length of the shadow of a pole is equal to a height of the pole then the elevation of light is?
Hence, the angle elevation is 45o.
Q. When the length of the shadow of a pole is equal to its height the elevation at Source of sight is?
ATQ, The height of pillar, and the length of the shadow are equal to each other. Therefore, the angle of elevation of the pillar from the source of sight is 45°, making the answer Option(b) 45°. Therefore the angle of elevation is 45°.
Q. What is the altitude of the sun if the length of the shadow and height of the object from the ground are equal?
when the length of the shadow of vertical pole is equal to its own height the sun would be 45 degree.
Q. When the length of shadow of a vertical pole is equal to v3 times of its height the angle of elevation of the sun’s altitude is?
Answer Expert Verified Let the height of the pole ( AB) = h . Let ϴ denotes the angle of elevation of the Sun. Hence , the angle of elevation of the Sun is 30 °.
Q. When the length of the shadow of a vertical pole is equal to √ 3?
We have been given that the height of the pole is √3 times the length of the shadow. Let the length of the shadow be h, then the height of the pole will be √3h. From the figure it is clear that the angle of elevation of the sun will be the angle of the line ED from the ground level.
Q. When the length of the shadow of a pole of height 7m?
Answer. The elevation then will be 90° as shadow is equal to pole.
