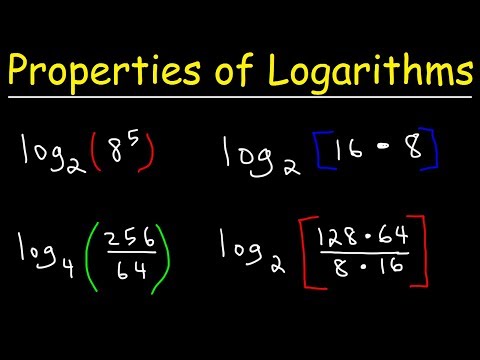Some important properties of logarithms are given here. First, the following properties are easy to prove. For example, log51= 0 l o g 5 1 = 0 since 50 =1 5 0 = 1 and log55 =1 l o g 5 5 = 1 since 51 =5 5 1 = 5.

The natural logarithm of any negative number is undefined. The natural logarithm of zero, that is, is also undefined: The natural logarithm of 1 is equal to zero: The natural logarithm of infinity is equal to infinity: The natural logarithm of the natural number, e, is equal to 1:

We can use the product rule to rewrite logarithmic expressions. For our purposes, expanding a logarithm means writing it as the sum of two logarithms or more. Let’s expand . Notice that the two factors of the argument of the logarithm are and . We can directly apply the product rule to expand the log.

The power rule for logarithms can be used to simplify the logarithm of a power by rewriting it as the product of the exponent times the logarithm of the base. Express the argument as a power, if needed. Write the equivalent expression by multiplying the exponent times the logarithm of the base. Rewrite log2x5 l o g 2 x 5.

As you can see these log properties are very much similar to laws of exponents. Let us compare here both the properties using a table: The natural log (ln) follows the same properties as the base logarithms do. The application of logarithms is enormous inside as well as outside the mathematics subject.

For example, log51= 0 l o g 5 1 = 0 since 50 =1 5 0 = 1 and log55 =1 l o g 5 5 = 1 since 51 =5 5 1 = 5. Next, we have the inverse property.