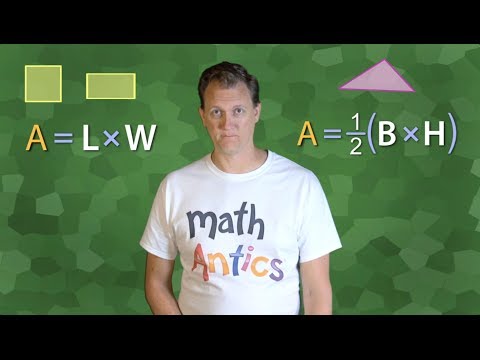Area is a measure of how much space there is inside a shape. Calculating the area of a shape or surface can be useful in everyday life – for example you may need to know how much paint to buy to cover a wall or how much grass seed you need to sow a lawn.

What real-life situations require us to use area? ▫ Floor covering, like carpets and tiles, require area measurements. Wallpaper and paint also call for area measurements. Fabric used for clothing and other items also demand that length and width be considered.

Area is measured in square units such as square inches, square feet or square meters. To find the area of a rectangle, multiply the length by the width. The formula is: A = L * W where A is the area, L is the length, W is the width, and * means multiply.

In Maths, the mean is defined as the average of all the given values. It means how far the data values are spread out from the mean value. The standard deviation measures the absolute variability of the distribution of the data.

A standard deviation is a statistic that measures the dispersion of a dataset relative to its mean. The standard deviation is calculated as the square root of variance by determining each data point’s deviation relative to the mean.

A normal distribution with a mean of 0 and a standard deviation of 1 is called a standard normal distribution. Areas of the normal distribution are often represented by tables of the standard normal distribution. For example, a Z of -2.5 represents a value 2.5 standard deviations below the mean.

σ

A standard deviation (or σ) is a measure of how dispersed the data is in relation to the mean. Low standard deviation means data are clustered around the mean, and high standard deviation indicates data are more spread out.

For an approximately normal data set, the values within one standard deviation of the mean account for about 68% of the set; while within two standard deviations account for about 95%; and within three standard deviations account for about 99.7%.

Standard deviation is a number used to tell how measurements for a group are spread out from the average (mean or expected value). A low standard deviation means that most of the numbers are close to the average, while a high standard deviation means that the numbers are more spread out.

Things like heights of people in a particular population tend to roughly follow a normal distribution. Standard deviations are important here because the shape of a normal curve is determined by its mean and standard deviation. The mean tells you where the middle, highest part of the curve should go.

For an approximate answer, please estimate your coefficient of variation (CV=standard deviation / mean). As a rule of thumb, a CV >= 1 indicates a relatively high variation, while a CV < 1 can be considered low. A “good” SD depends if you expect your distribution to be centered or spread out around the mean.

A standard deviation can range from 0 to infinity. A standard deviation of 0 means that a list of numbers are all equal -they don’t lie apart to any extent at all.

Since we are working with real numbers, the only way for this to occur is for every one of the squared deviations to be equal to zero. This means that for every i, the term (xi – x )2 = 0. This means that every data value is equal to the mean.

As soon as you have at least two numbers in the data set which are not exactly equal to one another, standard deviation has to be greater than zero – positive. Under no circumstances can standard deviation be negative.

Can you find standard deviation of negative numbers? While standard deviation (the result) can’t be negative, the individual numbers that you calculate standard deviation for can reach any value, including negative.

The standard deviation provides a measure of the overall variation in a data set. The standard deviation is always positive or zero.

An individual measurement may be accurate or inaccurate, depending on how close it is to the true value. If the experimental value is less than the accepted value, the error is negative. If the experimental value is larger than the accepted value, the error is positive.

Sometimes, the Experimental value may be a smaller than the accepted value(theoretical value), then the error obtained is negative. If the experimental value is more than the accepted value, then the obtained error is positive.

If your calculation results in a negative percentage, the minus sign can be ignored. For example, if you get a percentage difference of -5, you would say the percentage difference is considered 5 percent rather than -5 percent.