Knowing about half-lives is important because it enables you to determine when a sample of radioactive material is safe to handle. They need to be active long enough to treat the condition, but they should also have a short enough half-life so that they don’t injure healthy cells and organs.
Q. How does half-life affect radioactivity?
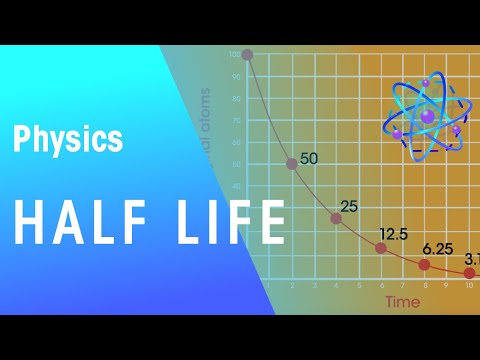
The longer the half-life of a nucleus, the lower the radioactive activity. A nucleus with a half-life that is a million times greater than another will be a million times less radioactive. A ‘half-life’ is defined as the amount of time taken for the number of nuclei present in a sample at a given time to exactly halve.
Table of Contents
- Q. How does half-life affect radioactivity?
- Q. How does the number of atoms present affect the half-life?
- Q. What is the half-life of a radioactive isotope?
- Q. How do you explain Half Life?
- Q. How do we use radioactive half life in real life?
- Q. How much technetium 99m remains in a human body after 12 hours after 24 hours?
- Q. What is the equation for radioactive decay?
- Q. How do you calculate 1/2 life of a drug?
- Q. How do you calculate two half lives?
- Q. How do you solve radioactive decay equations?
- Q. What is the equation for alpha decay?
- Q. What is rate of decay?
- Q. How do you calculate decay?
- Q. What are examples of radioactive decay?
- Q. What is decay chart?
- Q. What is decay constant?
- Q. How long will it take for 69% of a sample to decay?
- Q. How much time does it take for half of the atoms in a sample to decay?
- Q. What percentage of carbon-14 remains after 2 half lives?
- Q. Is the length of time required for one half of an isotope to decay?
Q. How does the number of atoms present affect the half-life?
No, the half-life defines the ratio and the number of stable atoms. The percent of decrease is the same no matter how many atoms you start with. By looking at the ratio of carbon-12 to carbon-14, they can calculate back to the amount of original carbon-14 using the carbon-14 half-life of 5,730 years.
Q. What is the half-life of a radioactive isotope?
The half-life of a radioactive isotope is the amount of time it takes for one-half of the radioactive isotope to decay. The half-life of a specific radioactive isotope is constant; it is unaffected by conditions and is independent of the initial amount of that isotope.
Q. How do you explain Half Life?
Half-life (symbol t1⁄2) is the time required for a quantity to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable atoms survive.
Q. How do we use radioactive half life in real life?
Scientists can use their knowledge of radioactive decay and half-lives to determine the age of many things, including skeletal remains. One method used to determine the age of bones is the Carbon-14 method. Carbon-14 is a radioactive isotope of carbon that is found in all living things.
Q. How much technetium 99m remains in a human body after 12 hours after 24 hours?
After 6 hours, there will be only 50-mg of technetium-99m. After 12 hours, the amount will half again and there will be 25-mg of technetium left.
Q. What is the equation for radioactive decay?
Radioactive decay law: N = N.e-λt The rate of nuclear decay is also measured in terms of half-lives. The half-life is the amount of time it takes for a given isotope to lose half of its radioactivity. If a radioisotope has a half-life of 14 days, half of its atoms will have decayed within 14 days.
Q. How do you calculate 1/2 life of a drug?
Half-life (t½) is the time required to reduce the concentration of a drug by half. The formula for half-life is (t½ = 0.693 × Vd /CL) Volume of distribution (Vd) and clearance (CL) are required to calculate this variable.
Q. How do you calculate two half lives?
As you can see from this table, the amount of reactant left after n half-lives of a first-order reaction is (1/2) n times the initial concentration….Half-Lives.
| Number of Half-Lives | Percentage of Reactant Remaining | |
|---|---|---|
| 1 | 100%2=50% | 12(100%)=50% |
| 2 | 50%2=25% | 12(12)(100%)=25% |
| 3 | 25%2=12.5% | 12(12)(12)(100%)=12.5% |
| n | 100%2n | (12)n(100%)=(12)n% |
Q. How do you solve radioactive decay equations?
Average number of radioactive decays per unit time (rate) • or – Change in number of radioactive nuclei present: A = -dN/dt • Depends on number of nuclei present (N). During decay of a given sample, A will decrease with time.
Q. What is the equation for alpha decay?
An example will show the use of this equation. For the decay reaction 238U → 234Th + 4He, the mass values for 238U and 4He are in Table 3.1; for 234Th it is 234.043 594. Thus we obtain Qα = –931.5 (234.043 594 + 4.002 603 – 238.050 7785) = 4.274 MeV.
Q. What is rate of decay?
The rate of decay, or activity, of a sample of a radioactive substance is the decrease in the number of radioactive nuclei per unit time.
Q. How do you calculate decay?
Suppose N is the size of a population of radioactive atoms at a given time t, and dN is the amount by which the population decreases in time dt; then the rate of change is given by the equation dN/dt = −λN, where λ is the decay constant.
Q. What are examples of radioactive decay?
decay chainThe series of decays or transformations that radionuclides go through before reaching a stable form. For example, the decay chain that begins with Uranium-238 culminates in Lead-206, after forming intermediates such as Uranium-234, Thorium-230, Radium-226, and Radon-222. Also called the “decay series.”.
Q. What is decay chart?
When a radioactive substance decays, it emits particles from the nucleus in a effort to become a stable atom. To fill in the chart, a periodic table of the elements is needed. If an alpha particle is emitted, the atomic number decreases by 2 which will produce a new element.
Q. What is decay constant?
Definition. The decay constant (symbol: λ and units: s−1 or a−1) of a radioactive nuclide is its probability of decay per unit time. The number of parent nuclides P therefore decreases with time t as dP/P dt = −λ.
Q. How long will it take for 69% of a sample to decay?
Half-life is the time required for half the atoms in a sample to decay. Example (answers may vary): For C-14, the half-life is 5770 years. A 10-g sample of C-14 would contain 5 g of C-14 after 5770 years; a 0.20-g sample of C-14 would contain 0.10 g after 5770 years.
Q. How much time does it take for half of the atoms in a sample to decay?
A more precise definition of half-life is that each nucleus has a 50% chance of living for a time equal to one half-life t1/2. Thus, if N is reasonably large, half of the original nuclei decay in a time of one half-life.
Q. What percentage of carbon-14 remains after 2 half lives?
25 percent
Q. Is the length of time required for one half of an isotope to decay?
Explanation: The “half-life” of a sample of radioactive isotope is defined as the amount of time it takes for half of the nuclei in the sample to decay. This is called Carbon Dating, and is accurate out to about 50,000 years (about 10 half-lives).