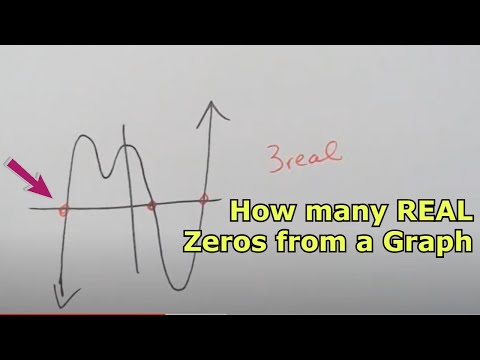
Follow these directions to find the intercepts and the zero.
Q. What is a double zero on a graph?
A double zero results from a function having a repeated root, for example: roots derived from factors of the form (x-a)^2. At the point of the root, the graph doesn’t cross the x axis (because a quadratic function governs that portion of the graph) but instead bounces back from the x axis.
Table of Contents
- Q. What is a double zero on a graph?
- Q. How do you tell if a graph has a double root?
- Q. What are real zeros?
- Q. Can real zeros be negative?
- Q. What are negative real zeros?
- Q. What is a positive real zero?
- Q. What are real roots in quadratic equation?
- Q. What are real and non real roots?
- Q. What equations have no real roots?
Q. How do you tell if a graph has a double root?
At a double root, the graph does not cross the x-axis. It just touches it. A double root occurs when the quadratic is a perfect square trinomial: x2 ±2ax + a2; that is, when the quadratic is the square of a binomial: (x ± a)2.
- Look for the y-intercept where the graph crosses the y-axis.
- Look for the x-intercept where the graph crosses the x-axis.
- Look for the zeros of the linear function where the y-value is zero.
Q. What are real zeros?
A real zero of a function is a real number that makes the value of the function equal to zero. A real number, r , is a zero of a function f , if f(r)=0 . Example: f(x)=x2−3x+2. Find x such that f(x)=0 .
Q. Can real zeros be negative?
This means there are no negative real zeros. Since we are counting the number of possible real zeros, 0 is the lowest number that we can have. This will help us narrow things down in the next step.
Q. What are negative real zeros?
Descartes’ rule of sign is used to determine the number of real zeros of a polynomial function. The number of negative real zeroes of the f(x) is the same as the number of changes in sign of the coefficients of the terms of f(-x) or less than this by an even number. …
Q. What is a positive real zero?
Example Questions Explanation: In order to determine the positive number of real zeroes, we must count the number of sign changes in the coefficients of the terms of the polynomial. The number of real zeroes can then be any positive difference of that number and a positive multiple of two.
Q. What are real roots in quadratic equation?
For an equation ax2+bx+c = 0, b2-4ac is called the discriminant and helps in determining the nature of the roots of a quadratic equation. If b2-4ac > 0, the roots are real and distinct. If b2-4ac = 0, the roots are real and equal. If b2-4ac < 0, the roots are not real (they are complex).
Q. What are real and non real roots?
The difference between real and imaginary roots: Real roots are the values of x where the graph of the function actually crosses the x-axis. Real roots are any roots that don’t have an “i” term. Imaginary roots are values of x that make the function equal zero, but the graph doesn’t actually cross the x-axis.
Q. What equations have no real roots?
Case 1: No Real Roots Since the quadratic formula requires taking the square root of the discriminant, a negative discriminant creates a problem because the square root of a negative number is not defined over the real line. An example of a quadratic function with no real roots is given by, f(x) = x2 − 3x + 4.